
Adana-Osmaniye-Hatay-Gaziantep üçlü birleşim bölgesi civarındaki güncel tektonik deformasyonların yarım uzay modellemesi ile belirlenmesi
Eylül 12, 2022
Sahte kimlikle başkasının arsasını sattı
Eylül 13, 2022Özet Bilgi
1. Giriş
Günümüzde, inşaat için haritaların üretiminde
şehir ve kasaba imar planları ve ilk tesiste
kadastro işlerinde havuzlarla karşılaşmak veya
dairesel formdaki binalar. Başka birine bağlandıktan sonra
elektronik takometre takılı çokgen
alana kurulan poligon noktasının koordinatları
ölçüm noktaları jeodezik hale getirilerek elde edilebilir
en az üç farklı noktadaki ölçümler
dairesel havuz veya bina. Çizim yardımı ile
haritacılık ile ilgili programlar (Netcad, Carto gibi
CAD, GEOCAD ...), elde etmek mümkündür
bir dairenin merkezinin koordinatları ve bunun yarıçapı
koordinatları bu üç noktadan daire içine alın
bilgisayar ortamında da hesaplanabilir.
Bu bilgilere erişmek mümkün değildir
haritacılık için haritalama programları
bir koordinat sistemindeki üç noktadan bir alanı geçirme,
çemberin merkezinin koordinatları ve çemberin yarıçapı
circle, yazılım şirketleri tarafından tescilli tutulur. Biz
merkezin koordinatlarının nasıl olduğunu merak ettiniz mi
bir dairenin veya söz konusu dairenin yarıçapı
bir bilgisayardaki alt programlar kullanılarak hesaplanır.
Bu sorunun çözümü ile ilgili olarak, iki çalışma
söz konusu konuya dolaylı olarak yakın olan
uygulama tanımlanmıştır (Kåsa, 1976; Coppe, 1993).
Ancak, bu çalışmaların doğrudan yapılmadığı tespit edilmiştir
araştırma konumuzu aydınlatın, bu nedenle bu konu şöyle olmalıdır
araştırıldı. Uygulamada herhangi bir çalışma bulunmadığından
bu sorunun çözümü ile ilgili olarak, şunları yapmak gerekir
bu sorunu araştırın. Bu çalışma teorik olarak sunulmuştur
konuya ilişkin çözümler, sayısal uygulamalar yapar
ve bulgular ve yorumlar sağlar.
Bu çalışmada yeni bir yöntem önerilmemiştir. Olarak
çalışmanın temel prensibi, bir dairenin geçişi
üç nokta ile, elde etme detayları
koordinatlar ve dairenin merkezinin yarıçapı
yazılım tarafından gizli tutuldukları için açıklığa kavuşturulması amaçlanmıştır
şirketler.
Haritacılık ile ilgili saha çalışmalarında her zaman
dairesel bir havuz çizimi ile karşılaşmak mümkündür ve
uygulamada bina. Bu nedenle, ilgili yazılım kullanılır
uygulayıcılar tarafından. Diğer ilgili içeriklerden bu yana
yazılım ilgili ticari tarafından gizli tutulur
şirketler, içinde ne tür sorunlar olduğu bilinmiyor
diğer yazılımlar ve hesaplamalar. Bu çalışmada teorik
konu ile ilgili çözümler sunulmakta ve sayısal
başvurular sağlanmaktadır.
Bu çalışmanın amacı;
polar ölçümleri yapılmış bir daire üzerinde üç nokta
bir poligon noktasından ve koordinatlarını bulun
çemberin merkezi ve yarıçapından yararlanarak
geometrik konumlar.
Koordinatları bulduktan sonra
daire üzerindeki noktalar, daire denklemi ile çözülebilir
bu noktaların koordinatlarının yardımı ve
dairenin merkezinin koordinatları şu adreste bulunabilir
dolaylı önlemlerin en azından dengelenmesine atıfta bulunmak
kareler yöntemi. Bununla birlikte, böyle bir çözüm çok zaman alır
bu çalışmada belirtilen yönteme kıyasla zaman.
2. HESAPLAMA
ÖLÇÜM KOORDİNATLARI
ÇOKGEN BİR NOKTADAN NOKTALAR
ÜÇ NOKTALI KUTUPLARA
BİR DAİRE ÜZERİNDEKİ ÖLÇÜMLER
Dairesel bir havuzun veya binanın yakınında, bir
elektronik takometre önceden kurulmuş bir
kurulan P1 çokgen sitesi ve başka bir bağlantı
önceden belirlenmiş P2 noktası yapılır. Üç ayrı
havuzun yakınındaki raylarda noktalar (A, B, C) işaretlenir veya
binanın zemini. Yatay açılar ve yatay
mesafeler (ßA, ßB, ßC, SA, SB, SC) tutularak ölçülür
işaretli nokta yansıtıcısı (Şekil 1).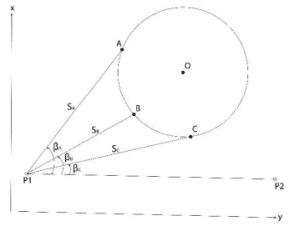
(P1P2)=arctan(
𝒀𝟐−𝒀𝟏
𝑿𝟐−𝟏
) (1)
(P1A)=(P1P2)-βA (2)
(P1B)=(P1P2)-βB (3)
(P1C)=(P1P2)-βC (4)
YA =Y1 + SA*sin (P1A), XA = X1 + SA*cos (P1A) (5)
YB =Y1 + SB*sin (P1B), XB = X1 + SB*cos (P1B) (6)
YC =Y1 + SC*sin (P1C), XC = X1 + SC*cos (P1C) (7)
AB ve BC akor uzunlukları
aşağıdaki ilişkiler;![]()
Dördüncü nokta da işaretlenebilir ve ölçülebilir
dairesel havuzun veya binanın yakınındaki izleri kontrol edin.
zemin. Bu durumda, yatay açı ve yatay
dördüncü nokta için ölçülen mesafeler
yukarıdaki ilişkilere benzer şekilde oluşan ilişkiler,
dördüncü noktanın koordinatı ve ışın uzunluğu
en yakın ölçüm noktası arasında hesaplanabilir.
3. MERKEZİN HESAPLANMASI
A'nın KOORDİNATLARI VE YARIÇAPI
AKOR NOKTALARI İLE DAİRE
Akor noktaları daire üzerinde şu şekilde işaretlenebilir
eşit veya farklı akor uzunlukları.
3.1. Merkez Koordinatlarının ve Yarıçapının Hesaplanması
eşit Akor Uzunluklarında İşaretlenmiş Noktalara Sahip bir Daire
Daire üzerindeki noktalardaki akor uzunlukları eşitse
birbirlerine (AB = BC) (Şek. 2), daha sonra tabanın açıları
ikizkenar üçgenlerde A, B ve C (α) noktalarında oluşan
daire içinde birbirine eşit olacaktır.
Α ve ε açıları aşağıdakilerden elde edilir
ilişkiler (Allan ve ark., 1968; Anderson ve Mikhail, 1998;
Kavanagh, 2000; Kavanagh, 2003; Kavanagh, 2009; İnce
ve Erdem, 2019).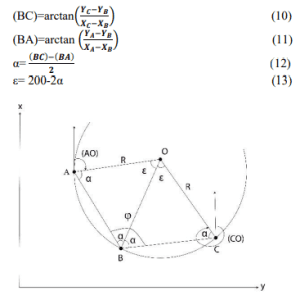
Şekil 2: Noktalarla işaretlenmiş yarıçap (R) hesabı
eşit akor uzunlukları.
Şekil 2'de, R = AO = BO = CO şu şekilde bulunur:
aşağıdaki ilişkiler;
Yatak açıları ((AO), (BO) ve (CO)) aşağıdaki gibidir:
A noktalarından aşağıdaki denklemlerden elde edilir,
B ve C'den O noktasına;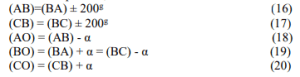
Çemberin merkezinin koordinatları (YO, XO) aşağıdaki gibidir:
aşağıdaki ilişkilerden türetilmiştir;![]()
(Bannister ve ark., 1992; Bannister ve diğ., 1998, Erdem ve
İnce, 2016)
3.2. Merkez Koordinatlarının ve Yarıçapının Hesaplanması
farklı Akor Uzunluklarında İşaretlenmiş Noktalara Sahip bir Daire
Üzerinde işaretlenmiş noktalar arasındaki akor uzunlukları ise
daire farklıdır, daha sonra taban açıları (α1, α2)
OAB ve OBC üçgenleri birbirine eşit değildir. İçinde
İncir. 3, BA ve BC akorları arasındaki açı (℃)
B ve α1 noktaları aşağıdaki ilişkilerle ifade edilir
(Kavanagh ve Kuş, 2000; Kavanagh, 2003; Kavanagh,
2009);
φ = (BC) - (BA)
α2 = φ - α1
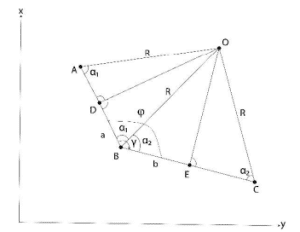
Şekil 3: Yarıçap (R) hesabı üzerinde işaretli noktalar
farklı akor uzunlukları.
Şekil 2 de;
a = AB/2 (26)
b = BC/2 (27)
D: AB akorunun orta noktası, E: AB akorunun orta noktası.
BC akoru ve aşağıdaki denklem R için yazılmıştır
odb'nin sağ üçgenleri ve BİR.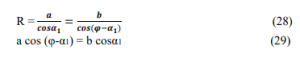
denklem (30) ile hesaplanan α1
R. α1 elde etmek için bağda (28) ikame edilir
ilişkide (25) ve α2 hesaplanır.(AO), (BO) ve
(CO), O, A ve B ve C noktalarını içerir
aşağıdaki denklemlerden elde edilir;
(AO) = (AB) - α1 (31)
(BO) = (BA) + α1 (32)
(BO) = (BC) - α2 (33)
(CO) = (CB) + α2 (34)
Çemberin merkezinin koordinatları (YO, XO) aşağıdaki gibidir:
ilişkilerle A, B ve C noktalarından elde edilen (21),
(22) ve (23) (Wilfred, 2001; Wolf ve Ghilani, 2008).


